Creating RSA Keys

---

In this chapter, we will focus on step wise implementation of RSA algorithm using Python.

Generating RSA keys

The following steps are involved in generating RSA keys −

• Create two large prime numbers namely p and q. The product of these numbers will be called n, where n= p*q
• Generate a random number which is relatively prime with (p-1) and (q-1). Let the number be called as e.
• Calculate the modular inverse of e. The calculated inverse will be called as d.

Algorithms for generating RSA keys

We need two primary algorithms for generating RSA keys using Python − Cryptomath module and Rabin Miller module.

Cryptomath Module

The source code of cryptomath module which follows all the basic implementation of RSA algorithm is as follows −

def gcd(a, b):
   while a != 0:
      a, b = b % a, a
   return b

def findModInverse(a, m):
   if gcd(a, m) != 1:
      return None
   u1, u2, u3 = 1, 0, a
   v1, v2, v3 = 0, 1, m
   
   while v3 != 0:
      q = u3 // v3
         v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
   return u1 % m

RabinMiller Module

The source code of RabinMiller module which follows all the basic implementation of RSA algorithm is as follows −

import random
def rabinMiller(num):
   s = num - 1
   t = 0
   
   while s % 2 == 0:
      s = s // 2
      t += 1
   for trials in range(5):
      a = random.randrange(2, num - 1)
      v = pow(a, s, num)
      if v != 1:
         i = 0
         while v != (num - 1):
            if i == t - 1:
               return False
            else:
               i = i + 1
               v = (v ** 2) % num
      return True
def isPrime(num):
   if (num 7< 2):
      return False
   lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 
   67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 
   157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 
   251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313,317, 331, 337, 347, 349, 
   353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 
   457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 
   571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 
   673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 
   797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 
   911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
	
   if num in lowPrimes:
      return True
   for prime in lowPrimes:
      if (num % prime == 0):
         return False
   return rabinMiller(num)
def generateLargePrime(keysize = 1024):
   while True:
      num = random.randrange(2**(keysize-1), 2**(keysize))
      if isPrime(num):
         return num

The complete code for generating RSA keys is as follows −

import random, sys, os, rabinMiller, cryptomath

def main():
   makeKeyFiles('RSA_demo', 1024)

def generateKey(keySize):
   # Step 1: Create two prime numbers, p and q. Calculate n = p * q.
   print('Generating p prime...')
   p = rabinMiller.generateLargePrime(keySize)
   print('Generating q prime...')
   q = rabinMiller.generateLargePrime(keySize)
   n = p * q
	
   # Step 2: Create a number e that is relatively prime to (p-1)*(q-1).
   print('Generating e that is relatively prime to (p-1)*(q-1)...')
   while True:
      e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
      if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
         break
   
   # Step 3: Calculate d, the mod inverse of e.
   print('Calculating d that is mod inverse of e...')
   d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
   publicKey = (n, e)
   privateKey = (n, d)
   print('Public key:', publicKey)
   print('Private key:', privateKey)
   return (publicKey, privateKey)

def makeKeyFiles(name, keySize):
   # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' 
      (where x is the value in name) with the the n,e and d,e integers written in them,
   # delimited by a comma.
   if os.path.exists('%s_pubkey.txt' % (name)) or os.path.exists('%s_privkey.txt' % (name)):
      sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt already exists! Use a different name or delete these files and re-run this program.' % (name, name))
   publicKey, privateKey = generateKey(keySize)
   print()
   print('The public key is a %s and a %s digit number.' % (len(str(publicKey[0])), len(str(publicKey[1])))) 
   print('Writing public key to file %s_pubkey.txt...' % (name))
   
   fo = open('%s_pubkey.txt' % (name), 'w')
	fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
   fo.close()
   print()
   print('The private key is a %s and a %s digit number.' % (len(str(publicKey[0])), len(str(publicKey[1]))))
   print('Writing private key to file %s_privkey.txt...' % (name))
   
   fo = open('%s_privkey.txt' % (name), 'w')
   fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
   fo.close()
# If makeRsaKeys.py is run (instead of imported as a module) call
# the main() function.
if __name__ == '__main__':
   main()

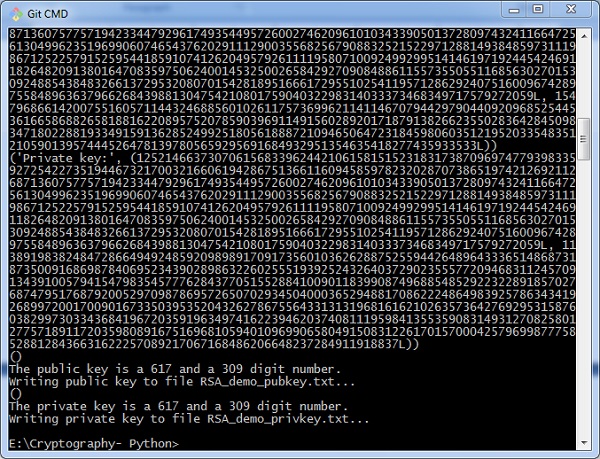
Output

The public key and private keys are generated and saved in the respective files as shown in the following output.